mathematics
overview
What is Mathematics?
Mathematics provides students with essential mathematical skills and knowledge in Number and Algebra, Measurement and Geometry, and Statistics and Probability. It develops the numeracy capabilities that all students need in their personal, work and civic life, and provides the fundamentals on which mathematical specialties and professional applications of mathematics are built.
The proficiency strands are Understanding, Fluency, Problem Solving, and Reasoning. They describe how content is explored or developed, that is, the thinking and doing of mathematics. They provide the language to build in the developmental aspects of the learning of mathematics and have been incorporated into the content descriptions of the three content strands described above. This approach has been adopted to ensure students’ proficiency in mathematical skills develops throughout the curriculum and becomes increasingly sophisticated over the years of schooling.
Content strands
Number and Algebra
Number and Algebra are developed together, as each enriches the study of the other. Students apply number sense and strategies for counting and representing numbers. They explore the magnitude and properties of numbers. They apply a range of strategies for computation and understand the connections between operations. They recognise patterns and understand the concepts of variable and function. They build on their understanding of the number system to describe relationships and formulate generalisations. They recognise equivalence and solve equations and inequalities. They apply their number and algebra skills to conduct investigations, solve problems and communicate their reasoning.
Measurement and Geometry
Measurement and Geometry are presented together to emphasise their relationship to each other, enhancing their practical relevance. Students develop an increasingly sophisticated understanding of size, shape, relative position and movement of two-dimensional figures in the plane and three-dimensional objects in space. They investigate properties and apply their understanding of them to define, compare and construct figures and objects. They learn to develop geometric arguments. They make meaningful measurements of quantities, choosing appropriate metric units of measurement. They build an understanding of the connections between units and calculate derived measures such as area, speed and density.
Statistics and Probability
Statistics and Probability initially develop in parallel and the curriculum then progressively builds the links between them. Students recognise and analyse data and draw inferences. They represent, summarise and interpret data and undertake purposeful investigations involving the collection and interpretation of data. They assess likelihood and assign probabilities using experimental and theoretical approaches. They develop an increasingly sophisticated ability to critically evaluate chance and data concepts and make reasoned judgments and decisions, as well as building skills to critically evaluate statistical information and develop intuitions about data.
Proficiency strands
The proficiency strands describe the actions in which students can engage when learning and using the content. While not all proficiency strands apply to every content description, they indicate the breadth of mathematical actions that teachers can emphasise.
Understanding
Students build a robust knowledge of adaptable and transferable mathematical concepts. They make connections between related concepts and progressively apply the familiar to develop new ideas. They develop an understanding of the relationship between the ‘why’ and the ‘how’ of mathematics. Students build understanding when they connect related ideas, when they represent concepts in different ways, when they identify commonalities and differences between aspects of content, when they describe their thinking mathematically and when they interpret mathematical information.
Fluency
Students develop skills in choosing appropriate procedures, carrying out procedures flexibly, accurately, efficiently and appropriately, and recalling factual knowledge and concepts readily. Students are fluent when they calculate answers efficiently, when they recognise robust ways of answering questions, when they choose appropriate methods and approximations, when they recall definitions and regularly use facts, and when they can manipulate expressions and equations to find solutions.
Problem Solving
Students develop the ability to make choices, interpret, formulate, model and investigate problem situations, and communicate solutions effectively. Students formulate and solve problems when they use mathematics to represent unfamiliar or meaningful situations, when they design investigations and plan their approaches, when they apply their existing strategies to seek solutions, and when they verify that their answers are reasonable.
Reasoning
Students develop an increasingly sophisticated capacity for logical thought and actions, such as analysing, proving, evaluating, explaining, inferring, justifying and generalising. Students are reasoning mathematically when they explain their thinking, when they deduce and justify strategies used and conclusions reached, when they adapt the known to the unknown, when they transfer learning from one context to another, when they prove that something is true or false and when they compare and contrast related ideas and explain their choices.
At Findon High School
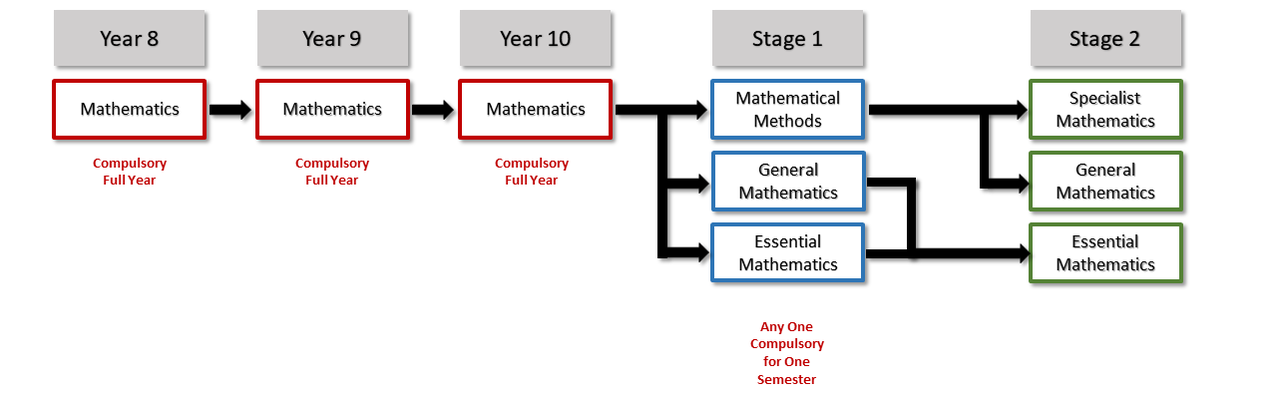
Mathematics is a compulsory full year subject for students in Years 8 to 10. Students are placed in “Advanced” and “Standard” programs from the second half of Year 8 onwards based on the results of their previous studies. Parents and students will have the opportunity to participate in this choice. In the senior school, one unit of Numeracy is compulsory at Year 11 (SACE Stage 1) and then Mathematics becomes an optional subject. However the particular level of Mathematics studied in the senior school is based on both career needs and recommendations from teachers based on achievement in previous years.
Mathematics provides students with essential mathematical skills and knowledge in Number and Algebra, Measurement and Geometry, and Statistics and Probability. It develops the numeracy capabilities that all students need in their personal, work and civic life, and provides the fundamentals on which mathematical specialties and professional applications of mathematics are built.
The proficiency strands are Understanding, Fluency, Problem Solving, and Reasoning. They describe how content is explored or developed, that is, the thinking and doing of mathematics. They provide the language to build in the developmental aspects of the learning of mathematics and have been incorporated into the content descriptions of the three content strands described above. This approach has been adopted to ensure students’ proficiency in mathematical skills develops throughout the curriculum and becomes increasingly sophisticated over the years of schooling.
Content strands
Number and Algebra
Number and Algebra are developed together, as each enriches the study of the other. Students apply number sense and strategies for counting and representing numbers. They explore the magnitude and properties of numbers. They apply a range of strategies for computation and understand the connections between operations. They recognise patterns and understand the concepts of variable and function. They build on their understanding of the number system to describe relationships and formulate generalisations. They recognise equivalence and solve equations and inequalities. They apply their number and algebra skills to conduct investigations, solve problems and communicate their reasoning.
Measurement and Geometry
Measurement and Geometry are presented together to emphasise their relationship to each other, enhancing their practical relevance. Students develop an increasingly sophisticated understanding of size, shape, relative position and movement of two-dimensional figures in the plane and three-dimensional objects in space. They investigate properties and apply their understanding of them to define, compare and construct figures and objects. They learn to develop geometric arguments. They make meaningful measurements of quantities, choosing appropriate metric units of measurement. They build an understanding of the connections between units and calculate derived measures such as area, speed and density.
Statistics and Probability
Statistics and Probability initially develop in parallel and the curriculum then progressively builds the links between them. Students recognise and analyse data and draw inferences. They represent, summarise and interpret data and undertake purposeful investigations involving the collection and interpretation of data. They assess likelihood and assign probabilities using experimental and theoretical approaches. They develop an increasingly sophisticated ability to critically evaluate chance and data concepts and make reasoned judgments and decisions, as well as building skills to critically evaluate statistical information and develop intuitions about data.
Proficiency strands
The proficiency strands describe the actions in which students can engage when learning and using the content. While not all proficiency strands apply to every content description, they indicate the breadth of mathematical actions that teachers can emphasise.
Understanding
Students build a robust knowledge of adaptable and transferable mathematical concepts. They make connections between related concepts and progressively apply the familiar to develop new ideas. They develop an understanding of the relationship between the ‘why’ and the ‘how’ of mathematics. Students build understanding when they connect related ideas, when they represent concepts in different ways, when they identify commonalities and differences between aspects of content, when they describe their thinking mathematically and when they interpret mathematical information.
Fluency
Students develop skills in choosing appropriate procedures, carrying out procedures flexibly, accurately, efficiently and appropriately, and recalling factual knowledge and concepts readily. Students are fluent when they calculate answers efficiently, when they recognise robust ways of answering questions, when they choose appropriate methods and approximations, when they recall definitions and regularly use facts, and when they can manipulate expressions and equations to find solutions.
Problem Solving
Students develop the ability to make choices, interpret, formulate, model and investigate problem situations, and communicate solutions effectively. Students formulate and solve problems when they use mathematics to represent unfamiliar or meaningful situations, when they design investigations and plan their approaches, when they apply their existing strategies to seek solutions, and when they verify that their answers are reasonable.
Reasoning
Students develop an increasingly sophisticated capacity for logical thought and actions, such as analysing, proving, evaluating, explaining, inferring, justifying and generalising. Students are reasoning mathematically when they explain their thinking, when they deduce and justify strategies used and conclusions reached, when they adapt the known to the unknown, when they transfer learning from one context to another, when they prove that something is true or false and when they compare and contrast related ideas and explain their choices.
At Findon High School
Mathematics is a compulsory full year subject for students in Years 8 to 10. Students are placed in “Advanced” and “Standard” programs from the second half of Year 8 onwards based on the results of their previous studies. Parents and students will have the opportunity to participate in this choice. In the senior school, one unit of Numeracy is compulsory at Year 11 (SACE Stage 1) and then Mathematics becomes an optional subject. However the particular level of Mathematics studied in the senior school is based on both career needs and recommendations from teachers based on achievement in previous years.
year 8 - mathematics - 8mth
CODE: 8MTH1, 8MTH2
SEMESTERS: 1 and 2
By the end of Year 8, students solve everyday problems involving rates, ratios and percentages. They recognise index laws and apply them to whole numbers. They describe rational and irrational numbers. Students solve problems involving profit and loss. They make connections between expanding and factorising algebraic expressions. Students solve problems relating to the volume of prisms. They make sense of time duration in real applications. They identify conditions for the congruence of triangles and deduce the properties of quadrilaterals. Students model authentic situations with two-way tables and Venn diagrams. They choose appropriate language to describe events and experiments. They explain issues related to the collection of data and the effect of outliers on means and medians in that data.
Students use efficient mental and written strategies to carry out the four operations with integers. They simplify a variety of algebraic expressions. They solve linear equations and graph linear relationships on the Cartesian plane. Students convert between units of measurement for area and volume. They perform calculations to determine perimeter and area of parallelograms, rhombuses and kites. They name the features of circles and calculate the areas and circumferences of circles. Students determine complementary events and calculate the sum of probabilities.
SEMESTERS: 1 and 2
By the end of Year 8, students solve everyday problems involving rates, ratios and percentages. They recognise index laws and apply them to whole numbers. They describe rational and irrational numbers. Students solve problems involving profit and loss. They make connections between expanding and factorising algebraic expressions. Students solve problems relating to the volume of prisms. They make sense of time duration in real applications. They identify conditions for the congruence of triangles and deduce the properties of quadrilaterals. Students model authentic situations with two-way tables and Venn diagrams. They choose appropriate language to describe events and experiments. They explain issues related to the collection of data and the effect of outliers on means and medians in that data.
Students use efficient mental and written strategies to carry out the four operations with integers. They simplify a variety of algebraic expressions. They solve linear equations and graph linear relationships on the Cartesian plane. Students convert between units of measurement for area and volume. They perform calculations to determine perimeter and area of parallelograms, rhombuses and kites. They name the features of circles and calculate the areas and circumferences of circles. Students determine complementary events and calculate the sum of probabilities.
- Based on ability and/or career interests, students are arranged into “Advanced” and “Standard” classes midway through Year 8. Typically students in an advanced Year 8 Mathematics class proceed to an advanced Year 9 and Year 10 Mathematics Class. This has implications for subject choices in Year 11. Please refer to the “Recommended Previous Studies” for the Stage 1 Mathematical Studies course below.
YEAR 9 - MATHEMATICS - 9MTH
CODE: 9MTH1, 9MTH2
SEMESTERS: 1 and 2
By the end of Year 9, students solve problems involving simple interest. They interpret ratio and scale factors in similar figures. Students explain similarity of triangles. They recognise the connections between similarity and the trigonometric ratios. Students compare techniques for collecting data in primary and secondary sources. They make sense of the position of the mean and median in skewed, symmetric and bi-modal displays to describe and interpret data.
Students apply the index laws to numbers and express numbers in scientific notation. They expand binomial expressions. They find the distance between two points on the Cartesian plane and the gradient and midpoint of a line segment. They sketch linear and non-linear relations. Students calculate areas of shapes and the volume and surface area of right prisms and cylinders. They use Pythagoras’ Theorem and trigonometry to find unknown sides of right-angled triangles. Students calculate relative frequencies to estimate probabilities, list outcomes for two-step experiments and assign probabilities for those outcomes. They construct histograms and back-to-back stem-and-leaf plots.
SEMESTERS: 1 and 2
By the end of Year 9, students solve problems involving simple interest. They interpret ratio and scale factors in similar figures. Students explain similarity of triangles. They recognise the connections between similarity and the trigonometric ratios. Students compare techniques for collecting data in primary and secondary sources. They make sense of the position of the mean and median in skewed, symmetric and bi-modal displays to describe and interpret data.
Students apply the index laws to numbers and express numbers in scientific notation. They expand binomial expressions. They find the distance between two points on the Cartesian plane and the gradient and midpoint of a line segment. They sketch linear and non-linear relations. Students calculate areas of shapes and the volume and surface area of right prisms and cylinders. They use Pythagoras’ Theorem and trigonometry to find unknown sides of right-angled triangles. Students calculate relative frequencies to estimate probabilities, list outcomes for two-step experiments and assign probabilities for those outcomes. They construct histograms and back-to-back stem-and-leaf plots.
YEAR 10 - MATHEMATICS - 0MTH
CODE: 0MTH1, 0MTH2, 0MTH3, 0MTH4
SEMESTERS: 1 and 2
By the end of Year 10, students recognise the connection between simple and compound interest. They solve problems involving linear equations and inequalities. They make the connections between algebraic and graphical representations of relations. Students solve surface area and volume problems relating to composite solids. They recognise the relationships between parallel and perpendicular lines. Students apply deductive reasoning to proofs and numerical exercises involving plane shapes. They compare data sets by referring to the shapes of the various data displays. They describe bivariate data where the independent variable is time. Students describe statistical relationships between two continuous variables. They evaluate statistical reports.
Students expand binomial expressions and factorise monic quadratic expressions. They find unknown values after substitution into formulas. They perform the four operations with simple algebraic fractions. Students solve simple quadratic equations and pairs of simultaneous equations. They use triangle and angle properties to prove congruence and similarity. Students use trigonometry to calculate unknown angles in right-angled triangles. Students list outcomes for multi-step chance experiments and assign probabilities for these experiments. They calculate quartiles and inter-quartile ranges.
There are three Mathematics subjects at Stage 2:
Each of these subjects assumes certain knowledge.
Students who want to learn mathematics with an emphasis on practical applications would take a course that leads to Mathematical Applications. Programs in this subject lead to post-compulsory courses in areas such as building and construction, aquaculture, agriculture, retail, office management, and visual arts.
Students who want to enter areas such as architecture, economics, finance, and biological, environmental, geological, and agricultural science should study a course that leads to Mathematical Studies.
Students who want to continue their studies in mathematics at the tertiary level in fields such as mathematical sciences, engineering, computer science, physical sciences, and surveying should take a course that leads to Specialist Mathematics. Students envisaging careers in other mathematically related fields would also benefit from studying a course that leads to Mathematical Studies and/or Specialist Mathematics.
For accurate information about post-compulsory courses, prerequisites, and assumed knowledge, students should consult current publications from the institutions or providers and the South Australian Tertiary Admissions Centre.
All programs at Stage 1 are required to incorporate the use of graphics calculators, to support classroom teaching, learning, and assessment.
SEMESTERS: 1 and 2
By the end of Year 10, students recognise the connection between simple and compound interest. They solve problems involving linear equations and inequalities. They make the connections between algebraic and graphical representations of relations. Students solve surface area and volume problems relating to composite solids. They recognise the relationships between parallel and perpendicular lines. Students apply deductive reasoning to proofs and numerical exercises involving plane shapes. They compare data sets by referring to the shapes of the various data displays. They describe bivariate data where the independent variable is time. Students describe statistical relationships between two continuous variables. They evaluate statistical reports.
Students expand binomial expressions and factorise monic quadratic expressions. They find unknown values after substitution into formulas. They perform the four operations with simple algebraic fractions. Students solve simple quadratic equations and pairs of simultaneous equations. They use triangle and angle properties to prove congruence and similarity. Students use trigonometry to calculate unknown angles in right-angled triangles. Students list outcomes for multi-step chance experiments and assign probabilities for these experiments. They calculate quartiles and inter-quartile ranges.
- Based on ability and/or career interests, students are arranged into “Advanced” and “Standard” classes. This has implications for subject choices in Year 11. Please refer to the “Recommended Previous Studies” for the Stage 1 Mathematical Studies course below.
There are three Mathematics subjects at Stage 2:
- Mathematical Applications
- Mathematics
- Specialist Mathematics
Each of these subjects assumes certain knowledge.
Students who want to learn mathematics with an emphasis on practical applications would take a course that leads to Mathematical Applications. Programs in this subject lead to post-compulsory courses in areas such as building and construction, aquaculture, agriculture, retail, office management, and visual arts.
Students who want to enter areas such as architecture, economics, finance, and biological, environmental, geological, and agricultural science should study a course that leads to Mathematical Studies.
Students who want to continue their studies in mathematics at the tertiary level in fields such as mathematical sciences, engineering, computer science, physical sciences, and surveying should take a course that leads to Specialist Mathematics. Students envisaging careers in other mathematically related fields would also benefit from studying a course that leads to Mathematical Studies and/or Specialist Mathematics.
For accurate information about post-compulsory courses, prerequisites, and assumed knowledge, students should consult current publications from the institutions or providers and the South Australian Tertiary Admissions Centre.
All programs at Stage 1 are required to incorporate the use of graphics calculators, to support classroom teaching, learning, and assessment.
Stage 1 - General mathematics - 1mxx
CODE:
SEMESTERS: 1 and 2
ALTERNATIVE: Mathematical Methods or Essential Mathematics
Advice to Students
General Mathematics replaced Mathematical Applications in 2016
Structure and Organisation:
General Mathematics is designed for those students who want to extend their mathematical skills beyond Year 10 level but whose future studies or employment pathways do not require knowledge of calculus. The subject is designed for students who have a wide range of educational and employment aspirations, including continuing their studies at university or TAFE.
Throughout the subject there is also an emphasis on the use and application of digital technologies.
General Mathematics aims to develop students’:
One or both units may be taken. Topics studied include: Earning and Spending, Measurement, Saving and Borrowing, Statistics.
SEMESTERS: 1 and 2
ALTERNATIVE: Mathematical Methods or Essential Mathematics
Advice to Students
General Mathematics replaced Mathematical Applications in 2016
Structure and Organisation:
General Mathematics is designed for those students who want to extend their mathematical skills beyond Year 10 level but whose future studies or employment pathways do not require knowledge of calculus. The subject is designed for students who have a wide range of educational and employment aspirations, including continuing their studies at university or TAFE.
Throughout the subject there is also an emphasis on the use and application of digital technologies.
General Mathematics aims to develop students’:
- understanding of concepts and techniques drawn from the topic areas of number and algebra, geometry and trigonometry, graphs and networks, and statistics
- ability to solve applied problems using concepts and techniques drawn from the topic areas of number and algebra, geometry and trigonometry, graphs and networks, and statistics
- reasoning and interpretive skills in mathematical and statistical contexts
- capacity to communicate the results of a mathematical or statistical problem-solving activity in a concise and systematic manner using appropriate mathematical and statistical language
- capacity to choose and use technology appropriately and efficiently
One or both units may be taken. Topics studied include: Earning and Spending, Measurement, Saving and Borrowing, Statistics.
stage 1 - mathematical methods - 1m
CODE:
SEMESTERS: 1 and 2
ALTERNATIVE: General Mathematics or Essential Mathematics
Advice to Students
Mathematical Methods replaced Mathematical Studies in 2016
Recommended Previous Studies:
A high level of achievement in Mathematics at Year 10
Prerequisites:
1MAT101 for 1MAT102
Structure and Organisation:
Mathematical Methods is structured over four units. The topics in Unit 1 build on students’ mathematical experience. The topics ‘Functions and graphs’, ‘Trigonometric functions’ and ‘Counting and probability’ all follow on from topics in the F-10 curriculum from the strands, Number and Algebra, Measurement and Geometry and Statistics and Probability. In Mathematical Methods there is a progression of content and applications in all areas. For example, in Unit 2 differential calculus is introduced, and then further developed in Unit 3 where integral calculus is introduced. Discrete probability distributions are introduced in Unit 3, and then continuous probability distributions and an introduction to statistical inference conclude Unit 4.
SEMESTERS: 1 and 2
ALTERNATIVE: General Mathematics or Essential Mathematics
Advice to Students
Mathematical Methods replaced Mathematical Studies in 2016
Recommended Previous Studies:
A high level of achievement in Mathematics at Year 10
Prerequisites:
1MAT101 for 1MAT102
Structure and Organisation:
Mathematical Methods is structured over four units. The topics in Unit 1 build on students’ mathematical experience. The topics ‘Functions and graphs’, ‘Trigonometric functions’ and ‘Counting and probability’ all follow on from topics in the F-10 curriculum from the strands, Number and Algebra, Measurement and Geometry and Statistics and Probability. In Mathematical Methods there is a progression of content and applications in all areas. For example, in Unit 2 differential calculus is introduced, and then further developed in Unit 3 where integral calculus is introduced. Discrete probability distributions are introduced in Unit 3, and then continuous probability distributions and an introduction to statistical inference conclude Unit 4.
stage 1 - essential mathematics - 1m
CODE:
SEMESTERS: 1 and 2
ALTERNATIVES: Mathematical Methods, General Mathematics
Advice to Students
Essential Mathematical Methods replaced Numeracy for Work and Community Life in 2016
A course designed for students who would find it impossible to meet the SACE numeracy component requirements from other Stage 1 Mathematics courses. Students should not intend to study Mathematics or Science at Stage 2.
Structure and Organisation:
Essential Mathematics aims to develop students’:
SEMESTERS: 1 and 2
ALTERNATIVES: Mathematical Methods, General Mathematics
Advice to Students
Essential Mathematical Methods replaced Numeracy for Work and Community Life in 2016
A course designed for students who would find it impossible to meet the SACE numeracy component requirements from other Stage 1 Mathematics courses. Students should not intend to study Mathematics or Science at Stage 2.
Structure and Organisation:
Essential Mathematics aims to develop students’:
- understanding of concepts and techniques drawn from mathematics and statistics
- ability to solve applied problems using concepts and techniques drawn from mathematics and statistics
- reasoning and interpretive skills in mathematical and statistical contexts
- capacity to communicate in a concise and systematic manner using appropriate mathematical and statistical language
- capacity to choose and use technology appropriately.
STAGE 2 - SPECIALIST MATHEMATICS
CODE: 2MSC20
SEMESTERS: 1 and 2
ALTERNATIVE: General Mathematics, Essential Mathematics
Prerequisites: 1MAT101, 1MAT102 and 1MAT103.
Students taking this subject must also take Stage 2 General Mathematics
Advice to Students:
It is envisaged that this subject will provide students with pathways into the universities’ courses in Mathematical Sciences, Engineering, Computer Science, Physical Sciences, and Surveying.
Structure and Organisation:
Topics studied include:
Assessment:
The assessment in Specialist Mathematics is comprised of two parts: a school-based component and an examination component. The school-based assessment, weighted at 50%, is made up of Skills and Applications Tasks and a Directed Investigation. The External Examination is also weighted at 50%.
SEMESTERS: 1 and 2
ALTERNATIVE: General Mathematics, Essential Mathematics
Prerequisites: 1MAT101, 1MAT102 and 1MAT103.
Students taking this subject must also take Stage 2 General Mathematics
Advice to Students:
It is envisaged that this subject will provide students with pathways into the universities’ courses in Mathematical Sciences, Engineering, Computer Science, Physical Sciences, and Surveying.
Structure and Organisation:
Topics studied include:
- Polynomials and Complex Numbers,
- Vectors and Geometry,
- Calculus,
- Differential Equations.
Assessment:
The assessment in Specialist Mathematics is comprised of two parts: a school-based component and an examination component. The school-based assessment, weighted at 50%, is made up of Skills and Applications Tasks and a Directed Investigation. The External Examination is also weighted at 50%.
STAGE 2 - GENERAL MATHEMATICS
CODE: 2MGM20
SEMESTERS 1 and 2
ALTERNATIVE: SPECIALIST MATHEMATICS, ESSENTIAL MATHEMATICS
Prerequisites: 1MAT101, 1MAT102 (1MAT103 if required)
Advice to Students:
Students who wish to enter areas such as Architecture, Economics, Biological, Environmental, Geological, and Agricultural Science should study Mathematical Studies. If studied in conjunction with Specialist Mathematics it will provide students with pathways into courses such as Mathematical Sciences, Engineering, Computer Science, Physical Sciences, and Surveying. For accurate information about courses, prerequisites, and assumed knowledge, students should consult current publications from the institutions or providers and the South Australian Tertiary Admissions Centre.
Structure and Organisation:
Topics studied include:
Assessment:
The assessment in Mathematical Studies is comprised of two parts: a school-based component and an examination component. The school-based assessment, weighted at 70%, is made up of Skills and Application Tasks and a Portfolio of Directed Investigations and/or a Project. The external examination is weighted at 30%.
SEMESTERS 1 and 2
ALTERNATIVE: SPECIALIST MATHEMATICS, ESSENTIAL MATHEMATICS
Prerequisites: 1MAT101, 1MAT102 (1MAT103 if required)
Advice to Students:
Students who wish to enter areas such as Architecture, Economics, Biological, Environmental, Geological, and Agricultural Science should study Mathematical Studies. If studied in conjunction with Specialist Mathematics it will provide students with pathways into courses such as Mathematical Sciences, Engineering, Computer Science, Physical Sciences, and Surveying. For accurate information about courses, prerequisites, and assumed knowledge, students should consult current publications from the institutions or providers and the South Australian Tertiary Admissions Centre.
Structure and Organisation:
Topics studied include:
- Working with Statistics,
- Working with Functions and Graphs using Calculus,
- Working with Linear Equations and Matrices
Assessment:
The assessment in Mathematical Studies is comprised of two parts: a school-based component and an examination component. The school-based assessment, weighted at 70%, is made up of Skills and Application Tasks and a Portfolio of Directed Investigations and/or a Project. The external examination is weighted at 30%.
STAGE 2 ESSENTIAL MATHEMATICS
CODE: 2MEM20
SEMESTERS: 1 and 2
ALTERNATIVE:
Prerequisites:
Any two of 1MAT110, 1MAT102, 1MCN101, 1MCN102 ie any two units of Stage 1 Mathematics
Advice to Students:
This subject leads to courses in retail, office management, small business, tourism, hospitality. For accurate information about courses, prerequisites, and assumed knowledge, students should consult current publications from the institutions or providers and the South Australian Tertiary Admissions Centre.
Structure and Organisation:
Topics studied include: Investments and Loans, Mathematics and Small Business, Statistics and Working with Data, Share Investments.
Assessment
Assessment in Mathematical Applications consists of the following components, weighted as shown:
SEMESTERS: 1 and 2
ALTERNATIVE:
Prerequisites:
Any two of 1MAT110, 1MAT102, 1MCN101, 1MCN102 ie any two units of Stage 1 Mathematics
Advice to Students:
This subject leads to courses in retail, office management, small business, tourism, hospitality. For accurate information about courses, prerequisites, and assumed knowledge, students should consult current publications from the institutions or providers and the South Australian Tertiary Admissions Centre.
Structure and Organisation:
Topics studied include: Investments and Loans, Mathematics and Small Business, Statistics and Working with Data, Share Investments.
Assessment
Assessment in Mathematical Applications consists of the following components, weighted as shown:
- Assessment Component 1: Skills and Applications Tasks (30%)
- Assessment Component 2: Portfolio (40%)
- Assessment Component 3: Examination (30%)